Public Key Infrastructure - I Needed To Be Needed

Background

I began creating the content of this page in 2018, principally to give a little insight to my then thirteen-year-old daughter of what I did at work. While reading, it may help to remember that much of the third-person narrative is targeted at Olivia. The article also proved helpful in validating that my subject matter area of expertise wasn’t severely compromised by my brain injury.

The intent of this page isn’t to explain PKI’s cryptographic purpose in anything other than lay-person terms, its unstructured flow of sub-topics makes it unsuitable as a learning resource, despite my previously enjoying giving PKI training to customers. On one particular training course at a bank in Amsterdam, I handed out flippant certificates to the delegates at course completion.

Upon reviewing some PKI reference material which had been published on the web, I felt the urge to write about how I interacted with PKI during my career. An example was updating a Wikipedia article a little, which can be viewed in my creating a “Capabilities” section in this Wikipedia PKI article.

PKI theory is notoriously difficult to convey – it seems to either makes perfect sense to people or sounds like gibberish. I consider the following to be the best video simplification of the fundamentals of PKI that I’ve come across.

Introduction

Every web site you log into with a password through a web browser relies upon PKI. Typical examples of web sites which follow this modus operandi are email with Microsoft / Google, shopping with eBay / Amazon and banking with HSBC / Barclays.

When accessing these services, a padlock appears in the browser’s address bar, indicating that all data transmitted between the endpoint (your computer or mobile device) and the target destination (web server) is encrypted during its transmission over the internet. The transmitted data could be travelling many thousands of miles, via cables crossing through multiple countries and beneath several oceans.

The encryption employed means that during logon to a web site, the password sent by your browser (client) to the web site (server) isn’t visible to any party eavesdropping on the communication. The two-way (bi-directional) relationship also means that the information sent from the server to the client (you) is encrypted; examples being emails, shopping purchases and banking transactions.

The address bar padlock evidences that the encryption protocol HTTPS is in use, this standard is entirely reliant upon PKI. Without PKI, the reasonably straightforward online experience of logging onto world wide web services and sending / receiving potentially sensitive information would be exponentially more complicated. Robert Hannigan, the director of the UK’s GCHQ as of my commencing this article, made the following statement about PKI’s underpinning of HTTPS: “Almost every aspect of life online relies on PKI.”

While HTTPS on the world wide web is the most widespread use of PKI, HTTPS was the least typical engagement that I worked on. Most often I was engaged on PKI projects to:

Secure WiFi authentication
Secure data at rest – such as word processor or spreadsheet documents
Secure email to enable evidencing of: a) the email came from the originator, b) it hasn’t been altered
Strong authentication – typically using a smart card rather than a username and password, to logon to a computer or a Virtual Private Network (VPN)
Make code (apps) secure, to ensure that they: a) haven’t been altered since creation, b) don’t include malicious payloads

In 2008 I wrote a white paper for Oxford Computer Group, giving an introduction to PKI for IT professionals. Alternatively, a more simplified lay person approach can be read throughout the remainder of this page.

Much descriptive material regarding PKI on the internet refers to making information secure between Alice and Bob, i.e. A to B. Often there’ll be a third-party referenced as C (Charlie) who is trying to compromise the information by eavesdropping or maliciously altering data. The example scenario is now evolved into transmitting data between A and B… while avoiding or omitting C.

There are two broad strands of cryptography, distinguished by their different approach to the use of keys (secrets) – symmetric and asymmetric. In symmetric key cryptography, the same key (a secret value such as a number) is used to encrypt a payload (data) into ciphertext, as that used to subsequently decrypt the ciphertext into plaintext. As an example, we’ll consider how to transmit the value 14 (plaintext) secretly in a message. You could multiply the plaintext by the number 5 (this number is the symmetric key). The multiplication operation is referred to as the algorithm [1]. The resultant encrypted (ciphertext) value would be 70. The same (symmetric) key value of 5 is used by the message recipient to decrypt the ciphertext, thus revealing the original plaintext payload of 14.

In asymmetric cryptography, a different key is used to decrypt the ciphertext from that used to previously encrypt the payload – this will be explained below! The bulk of this article is based upon asymmetric cryptography, as it’s the foundation of PKI.

[1] A realistic algorithm is significantly more complex. An example may be to square the payload (plaintext), then double it, then subtract 50, then multiply it by 7, and so on.

Trust Services

PKI is generally referred to in IT security as providing trust services. I have sometimes been employed as a trust services architect, a role I undertook for the UK Ministry of Defence (MoD) was exactly such. Trust services are typically employed to meet one of the following triad of capabilities: Confidentiality, Integrity and Authenticity – the acronym CIA is often used. The following is snipped from my Wikipedia entry.

a) Confidentiality: Certainty that no entity (person or computer) can view the payload (typically data) in plaintext – either maliciously or unwittingly. The payload is encrypted to make it secret, such that if it was read, it’d appear as gibberish.
b) Integrity: Certainty that if somebody or something changed (tampered) with data in even the slightest way, it’d be obvious, as its integrity would have been compromised. Often, it’s not of utmost importance to prevent the integrity being compromised (tamper proof). It’s typically more important that if integrity is compromised, there’s clear evidence of it having done so (tamper evident). Aligned with integrity is the concept of non-repudiation; by way of example, if you’ve said you’re going to do something, it must be impossible to refute (deny) having said it.
c) Authenticity: Certainty that only authenticated entities can access protected resources. Authenticity is often used to assert one’s identity when leveraging PKI during a logon process. Usernames and passwords have limitations which often render them too weak for mission critical authentication. Authenticity is also often used to prove that a communication (e.g. an email message) was originated by who claimed to have done so. There must be no opportunity for spoofing / impersonation / man-in-the-middle attacks to have occurred, e.g. someone cannot fake your credentials to logon as you.

Symmetric Key Cryptography

Before considering public key (asymmetric) cryptography, it’s useful to restate its counterpart. Symmetric key cryptography is extremely fast and efficient to encrypt large amounts of data, since no computation power is consumed by the cryptographic processing requirements of [3].

The principal disadvantage of symmetric key cryptography is that the key needs to be exchanged securely between partners for any encryption / decryption functions to be undertaken, this is done alongside the algorithm to be used (e.g. multiply). In all cryptographic capabilities there is a key, and an algorithm which is applied to the plaintext. The algorithm isn’t secret, since all sending and receiving parties need to know what maths to perform on: a) the plaintext, b) the subsequent ciphertext. In symmetric key crypto, the key itself is crucially important to make secret and transport securely between the sending and receiving parties, since if the key is discovered the value of symmetric key encryption is lost.

Asymmetric Key Cryptography

PKI leverages a mathematical construct referred to as asymmetric (unequal) cryptography, which uses one key to encrypt the plaintext and a different key to decrypt the ciphertext (encrypted plaintext). In asymmetric cryptography, the plaintext may be encrypted using a public key value of 91, but decryption of the ciphertext uses a different (but related) value, say 20. It sounds implausible, but on a purely conceptual level it does work in this way. In layman’s terms, the plaintext (data) is encrypted [2] to make a ciphertext by using a public key which anybody can know. However, the ciphertext can only be decrypted into plaintext with a private key which is known only by the recipient.

The public key is mathematically related to the private key. In this example, the public key (91) is the product of the prime numbers 7 and 13. The sum of the prime numbers is used as the private key (20). In real world application much larger values are used, such that it’s practically impossible [3] to computationally derive the private key from the public key. The public key is not required to have any protection whatsoever, you can email it or it can be posted on the internet – hence the term public. On the contrary, it’s of extreme importance to keep the private key secret. I was typically responsible for deploying customer solutions where the private key was stored in the gold chip on a smart card, making it very secret indeed. Only somebody with the PIN for the smart card (and physical possession of the smart card itself) could access the private key which was stored on it, and hence decrypt the ciphertext.

To muddy waters further, in real world use cryptography uses a combination of symmetric and asymmetric cryptography to achieve bulk encryption, i.e. performing it on large quantities of data.

Recap: symmetric encryption uses the same key to encrypt the plaintext and decrypt the ciphertext, whereas asymmetric encryption is where one key is used to encrypt plaintext and a different (but related) key is used to decrypt ciphertext.

[2] This explanation only applies to CONFIDENTIALITY purposes of PKI; for INTEGRITY and AUTHENTICATION purposes, the encrypting operation is performed with the private key.

[3] PKI typically utilises prime number factorisation or elliptic curve conjecture cryptography.

Cryptography Mathematics

The binary value of 64 bits (101010101010101010101010101010101010101010101010) equates to a decimal value of 187,649,984,473,770 – one hundred and eighty trillion or so. Each time a bit is added to a binary value it doubles, if two bits are added it quadruples. For example, if we started with the binary value 10 (decimal two) and added two binary bits to make 1110, we get decimal fourteen – roughly (very) quadruple two.

When it comes to PKI, bit lengths are used which sound insignificant in plain speak. For example, most of the PKIs I implemented had binary key lengths of 2,048 bits. However, when you consider that 64-bit binary values can equate to hundreds of trillions in decimal, and each additional binary bit length is roughly doubling the size of the decimal value, 2,048 bits is actually extremely large. PKI’s fundamental premise, and the reason it has long been considered unbreakable, is that it’s computationally implausible to mathematically derive the private key from the public key. Using Rivest Shamir Adleman (RSA) based algorithms (the most commonly used asymmetric cryptography algorithm in 2023), it’s necessary to calculate the two prime numbers between 1 and 187,649,984,473,770 (in this case) which are the factors of the key value. Another way of explaining the RSA algorithm’s strength is that it’s trivial to multiply two prime numbers together: 7901 times 7919 is 62,568,019. However, it’s difficult to start with the number 62,568,019 and work out which two prime numbers must be factored to produce it. The decimal value 187,649,984,473,770 in the given example is just 64 bits in length, whereas in reality a minimum of 2,048 bits would be used. Another approach to understanding the orders of magnitude involved with a 2,048 bit value is to think of one million as a 7 bit number, one billion as a 10 bit number and one trillion as a 13 bit number [4].

Everything I implemented beyond the year 2013 used 4,096 bit values, which is forecast by many standards bodies to be strong enough for hundreds of years to come, or until something called Quantum computing (see PKI Longevity section later) becomes reality. I’d estimate that 99% of the PKI work I did until 2018 was based upon RSA algorithms, which uses prime number factorisation. It’s likely there’ll be a transition from prime number factorisation to Elliptic Curve Cryptography (ECC) based algorithms. This approach isn’t because ECC has stronger security than RSA, but due to it requiring less compute power, which is important when considering the Internet of Things (IoT), i.e. small devices which have relatively small microprocessors.

[4] It’s an imprecise approach to compare binary and decimal values, but it does help illustrate the orders of magnitude of large bit length numbers.

Certification Authorities

Introduction

The principal customer deliverable during my career as a PKI consultant was the design, engineering, installation and commissioning of Certification Authorities.

A Certification Authority (CA) is an application installed on a server which creates digital certificates. Certificates are small files – typically 3KB in size, which are issued to subscribing entities such as users and computers. CAs which issue certificates to subscribing entities are referred to as Issuing CAs. Issuing CAs, in turn, have certificates issued to them by a parent CA – this results in a CA chain of trust, at the top of which is always the Root CA.

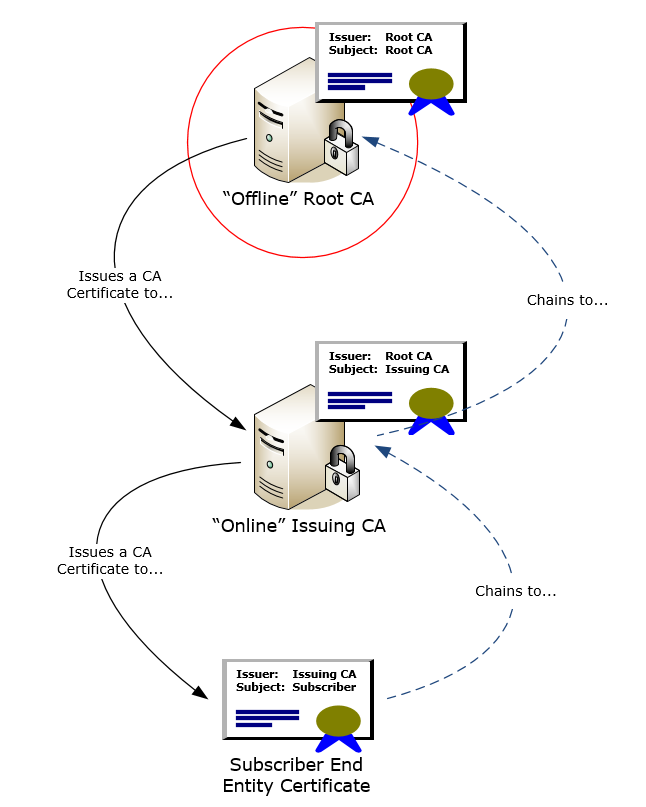
There are two streams of CAs: commercial CAs and private / corporate CAs. Commercial CAs are, in the main, used for issuance of digital certificates to servers on the world wide web, where they facilitate secure internet browsing by domestic users. Private / corporate CAs are typically used internally within an organisation such as a bank or government department. Private CAs are often utilised for a wider variety of purposes than commercial CAs, such as securing WiFi connections, encrypting data at rest (on file systems), strong user authentication, digital signing of code (software) and securing Virtual Private Networks (VPNs).

Root CA

Because the trust credibility of any PKI chains to its Root CA (often referred to as a trust anchor), extremely strong physical and logical security controls are implemented to protect its integrity. The most evident Root CA control is it being deployed and operated entirely offline of any networks. Benefits of this approach is that it’s invulnerable to network-based hacking attempts (logical), and can be stored in a safe deployed a long way from any network infrastructure (physical). From its very beginning, a server designated for Root CA purposes must never (even prior to operating system installation) have interaction with a network – either through cables or Wi-Fi. A Root CA typically never gets updated, and all material which it generates, such as the CA certificates (files) of its subordinate CAs are transferred via removable media. The Root CA itself has a designated validity period / operational longevity governed by a CA certificate – the majority of those I’ve designed have a lifetime of twenty years.

The limited operational requirements of a Root CA mean it only needs powering up on a periodic basis, such as every six or twelve months. Root CAs are typically operated in a dedicated location with very strong physical security and logical access controls, e.g. multiple thumb-print door access.

Commercial Root CA certificates are pre-installed into the operating systems of computers (Windows, Linux, etc.) and mobile devices (Android, iOS). It is the presence of Root CA certificates which underlies establishing of TLS channels when a client connects to a web site. This happens because the Issuing CA which issued the certificate to the web server, chains up to a Root CA (trust anchor) which is present on the computer / device where the connection is being established.

Issuing CAs

Issuing CAs, unlike Root CAs, need to be online on a network, such that they are available for issuance of digital certificates on a regular basis. Strong physical and logical security controls are still required for issuing CAs, however, they must be balanced against practical availability capabilities.

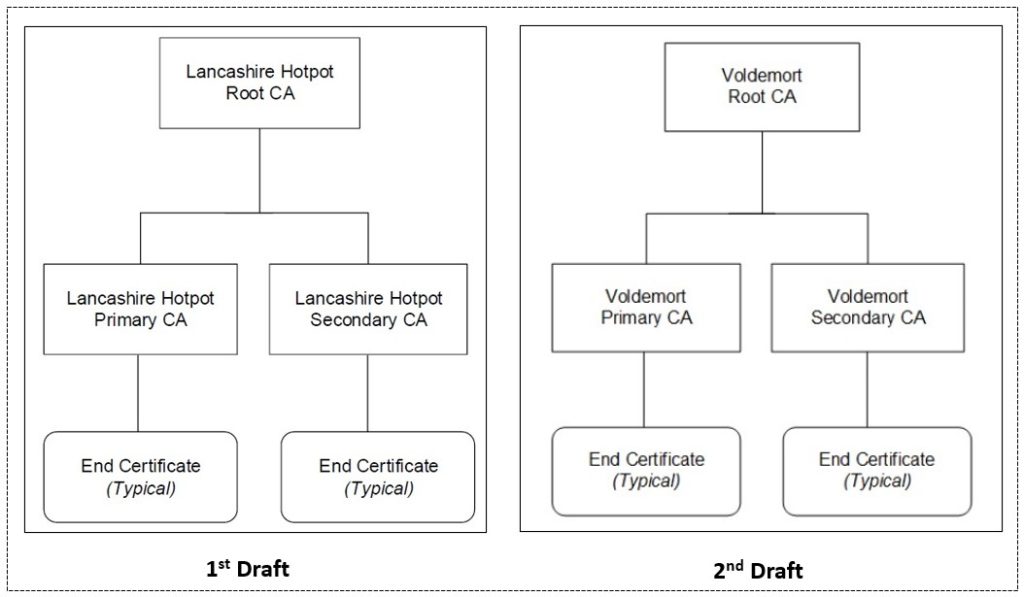
The adjacent diagram shows part of a draft CA hierarchy design I produced for a customer. The Primary CA and Secondary CA were Issuing CAs; the flippant names used here was part of a game I played with customers during the draft stage of PKI design. I often felt that customers dragged along too long to come up with suitable names for the CAs. My silly suggestions (when presented in formal documents) made it obvious that they to needed get a move on and come up with suitable names.

A typical scenario of an Issuing CA generating and disseminating a certificate to a subscribing party is as follows:

A subscribing entity generates a new pair of keys (one public and one private) on the subscribing device. The private key is created and stored in a secure manner, which may be a protected area of a computer’s operating system or in a dedicated hardware device, such as a smart card
The public key is transmitted on a network to an Issuing CA, along with information about the subscribing entity – such as its name
The Issuing CA creates a digital certificate, which contains the submitted public key and subject information
The Issuing CA digitally signs the certificate it has manufactured, using its own private key
The digital certificate is transmitted back to the subscribing entity, which goes through an exercise of joining the certificate (and embedded public key) with the private key which was created in the first step

Hardware Security Modules (HSMs)

The protection of a Certification Authority’s private key is of utmost importance to ensure the integrity of the entire certificate issuance process. Special purpose cryptographic devices known as Hardware Security Modules (HSMs) are used to store a CA’s private key in isolation of a server’s operating system. An HSM is a dedicated computing device, with its own operating system dedicated to its operational function. HSMs can either be directly attached to a CA server, or connected over a network using a dedicated and highly secure communication channel.

As well as the physical characteristics employed by HSMs to protect private keys, a range of logical controls are used. By way of example, initialisation (starting up) of a Root CA which leverages an HSM often mandates numerous separate persons must be involved in the process, such that a single rogue or compromised individual could not singularly start the CA.

When establishing the HSMs security characteristics, a group (or pool) of smart cards might be created which would be assigned to persons in a security enforcing role. Upon startup of a CA, each individual would require presentation of their smart card and the corresponding PIN to submit when challenged by the HSM software. In crypto authorisation semantics, the total number of cards in the pool is referred to as “N” and the quorum of cards required to be presented is “K”. By way of example, it might be deemed necessary that out of a pool of five potential designated participants, two must be present to facilitate initialisation of the CA; in this case the K of N would be 2 of 5.

The HSM smart cards aren’t typically stored by the individual, rather they’re kept in safes around the organisation, and the PINs would often be stored in different safes than the corresponding smart cards.

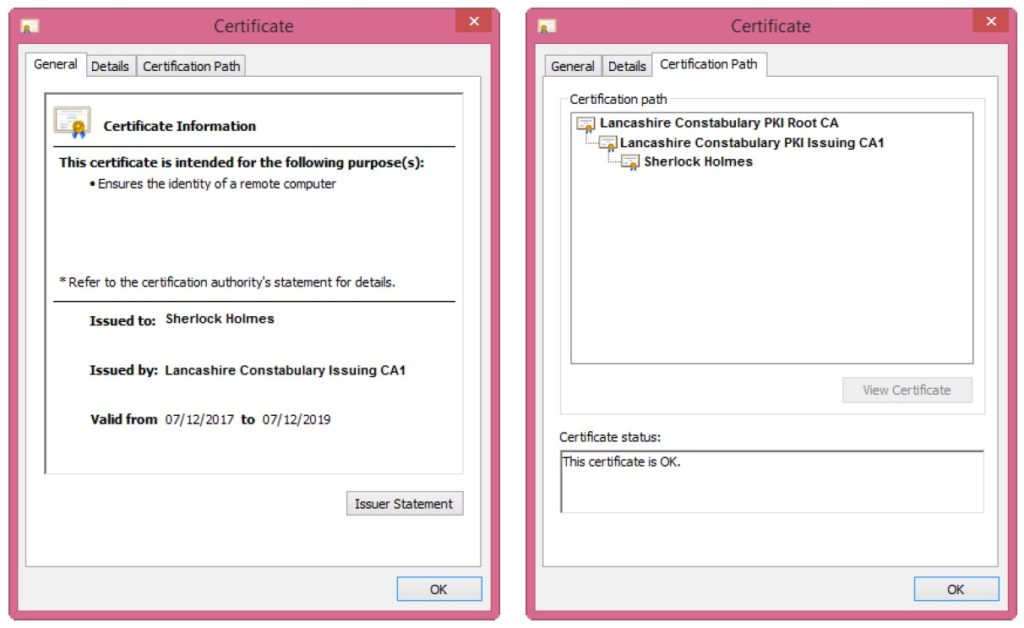
Digital Certificates

A digital certificate is issued by a Certification Authority (CA); it contains the subscriber’s (originating user or computer) public key and is stamped (digitally signed) by the CA’s private key. The simplest (and admittedly imprecise) analogy may be an envelope you send to an organisation containing your passport, in this circumstance:

The public key is your passport – which uniquely identifies you, it is placed into an envelope
The envelope is sealed with a sticker / stamped with red wax (this would be the digital signature)
The digital certificate is the envelope into which you place your passport

An important PKI concept to grasp is that when wanting to transmit an encrypted document (say), the sender must first obtain the target recipient’s public key, which is contained in the digital certificate. The party doing the encryption (sender) must use the recipient’s public key. Because the recipient possesses the private key associated with the public key embedded in the digital certificate, they can decrypt the document. Once the originator encrypts an email (say), even they can’t read the encrypted message, since they wouldn’t have access to the relevant private key.

While much of this page utilises written explanations of PKI processes, I thought it’d be helpful to interject a practical PKI use case video. The video here is one of my favourites, demonstrating the following processes:

Certificate enrolment by a user on the Windows operating system

Encryption of a Word document with the certificate (public key)

Demonstration of the consequence of losing access to the decryption (private) key

Recovery of the private key

Digital Hashing

A digital hash refers to taking a variable length input of any length, from as little as 10 characters to a 1,000-page bible (say), then passing its binary representation through an algorithm to produce a fixed length output of 160 or 256 bits (typically). The input length is always variable, and the output length is always fixed. If a hash was taken (and recorded) of the digital bible document, and then a single full stop (period) was added to the document, and the hash algorithm run again against its binary representation, the resulting hash would be entirely different from that generated for the original document. Digital hashes are the bedrock of integrity and authenticity, though they aren’t used in confidentiality.

Since about 2015, there was a concern regarding the strength of the prevalent algorithm named Secure Hash Algorithm 1 (SHA1), which produced a 160-bit output. In response to this, a newer algorithm was authorised (named SHA2), which uses a longer fixed length output, typically of 256 bits. When I helped implement Lancs’ PKI in 2010, I used SHA1, and that was a part of the reason they asked me to return in 2018, to redeploy their PKI based upon SHA2. At the Met I implemented their latest PKI in 2014 and had the foresight to insist on using SHA2, against the supposed better judgement of some senior Met IT security personnel. Amongst the challenges which the Met had to deal with during my absence due to my brain injury, a SHA1 to SHA2 migration wasn’t one of them.

Digital Signing

A digital signature is not an image / photo of a written signature – it’s a use of cryptography based upon PKI.

A concept to grasp is that securing data for CONFIDENTIALITY purposes uses the public key to encrypt data and the private key to decrypt it. However, anything other than CONFIDENTIALITY uses the opposite approach. In digital signatures (DigSig), which facilitate INTEGRITY and AUTHENTICITY, data is first hashed (using SHA2), then encrypted using a private key, before being sent to a recipient along with the original (unencrypted) document. The recipient subsequently uses the public key to decrypt the hash.

How this works is that the recipient uses the same SHA2 algorithm to create a hash of the attached unencrypted document, if the hash matches the value sent by the originator when hashing the document – bingo. From this outcome, it can be inferred that an email or document hasn’t been tampered with (INTEGRITY) and originated from who you thought it had (AUTHENTICITY). As usual, I have to state how this is a vast simplification (and slight deviation) of what is going on under the covers, but suffices as a basic conceptual explanation.

Cryptography Behind Password Authentication

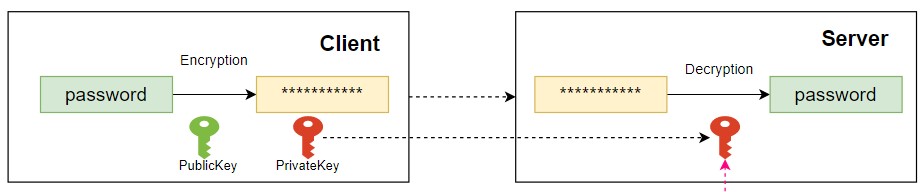
The following is a vast simplification of how a combination of PKI and digital hashing is used when creating passwords, and subsequently utilised during a typical web site logon process.

Creation of a New Password

A TLS encrypted channel is established between the client and the server to ensure that communications are confidential
The password entered into the browser on the local device is transmitted to the target web service (e.g. Barclays or Amazon) in the TLS channel
The web service creates a digital hash of the transmitted password
The web service stores the hash value in its database – the web service has no knowledge of the actual password value

Logging on to a Web Site

A TLS encrypted channel is established between the client and the server
The password is entered in the browser, whereby a digital hash of it is made
The digital hash is transmitted from the browser to the target web service in the TLS channel
The web service verifies that the hash value of the submitted password matches the one stored in its database

Hybrid Encryption

Asymmetric encryption is very compute expensive, as it takes many processor cycles to perform immense mathematical processing. A consequence of this is that it would take a very long time to purely use asymmetric cryptography to encrypt a lot of (bulk) data.

Pretty much all encryption which is done for data at rest (stored persistently – such as in a Word or Excel document on a file system) or in transit (such as when performing online banking with a browser) is a hybrid of asymmetric and symmetric cryptography. Symmetric cryptography is much quicker than asymmetric cryptography, so a symmetric key is created to do the bulk of the encryption of the document / transmission. In this circumstance, asymmetric cryptography is purely used to securely encrypt the symmetric key itself, to facilitate its secure exchange between the parties involved.

Key Signing Ceremony (KSC)

The term KSC is often most used in the context of the strict logical controls and procedures that need to be effected when deploying a new PKI, or undertaking activities on an existing PKI.

In combination with these logical controls are the necessary physical controls. In the photograph at the bottom of the page, which I took at a police data centre, there’s a desk and computer – which contained the Root CA. Often it was the case that as well as storing the equipment securely, customers would dictate that the actual KSC be performed in a secure storage facility – in this instance, it happened to be a cage.

Another important aspect of KSCs is to handle security sensitive material – smart cards and pass phrase forms, etc. in a secure manner. One piece of work I undertook for the Met Police in London’s New Scotland Yard required storing a Root CA securely. The tamper evident bags (a little like sandwich bags) which were used for most items (smart cards, USB sticks and password forms) were not large enough, so it was deemed necessary to use body bags for the purpose. I recall carrying a full body bag from one end of the NSY office buildings to the other.

PKI Origination

PKI is a mature mathematical concept, generally recognised to have been instantiated by Alan Turing in the WWII timeframe. Turing was a mathematics expert, who is generally considered to have helped reduce the length of World War II by several years. Turing, in tandem with Polish cryptographers discovered how to crack the German Enigma code, which enormously helped Britain and the US to defeat Nazi Germany. Despite Turing’s genius contributing to the saving of perhaps millions of lives, he was prosecuted and found guilty of being a homosexual. As punishment, he chose to be castrated in preference to being imprisoned for many years. He died at the age of 41, it was officially recorded as suicide. Following an internet campaign, in 2009 the then British Prime Minister (Gordon Brown) made a public apology for the way Turing was treated. Turing was given a posthumous pardon, whereby the government admitted it was wrong to have prosecuted Turing for the crimes (homosexuality) he was accused of.

We visited Bletchley Park (near to Milton Keynes) together in July 2019.

Blockchain Encryption

PKI has served me very well, but it’s a little too cumbersome for some future use cases, such as the Internet of Things (IoT). PKI scales to millions and even tens of millions of entities, but certainly not to the billions which IoT encompasses, which is expected to utilise a cryptographic capability which will likely supplant PKI: blockchain. This doesn’t mean PKI is dead, as blockchain may not be suitable for governments and banks, etc. which need the more robust trust basis which PKI provides. Blockchain will serve the masses (billions) and PKI will co-exist alongside it.

PKI Longevity

RSA algorithm is a fundamental bedrock of PKI, and has been in use since around since 1978. Despite the massive increases in computing power beyond that year, PKI remains almost universally recognised as the strongest means (in 2023) to keep information secure on the internet. PKI is about more than just the internet, I’d suggest that the majority of secret documents in the UK, US and European governments / military organisations are protected in some part by PKI.

A new method of computation named Quantum computing, is a huge threat to PKI as it’s currently implemented. Since their invention, computers have relied upon binary mathematical theory, whereby something (a bit) can either be on or off, typically a one or a zero. Quantum computing uses a different premise, whereby something can be in various states, not simply on / off. The best analogy I can make is that it can be likened to a coin being flipped, which ends as heads or tails (i.e. 0 or 1), but during the flipping phase is at various states during its rotation. The coin rotation could be measured in degrees (360 in a circle) and by 60 minutes in each degree and by a further 60 seconds in each minute. In this analogy, a simple coin-flip could have approximately 1.3 million (360 x 60 x 60) outcomes. It requires enormous expense to implement and some uncertainty of its actuality, however, there’s some inevitability that quantum computing will happen.

The hope is that the good guys (non-adversarial nation states), learn how to harness quantum cryptography before the bad guys do. I draw an analogy with the development of nuclear bombs; it was extremely important that the USA (allied with Western Europe) gained nuclear supremacy before the Soviet Union did. If Stalin’s Soviet scientists had attained nuclear supremacy over the west, it’s likely that our lifetime of freedom would have been significantly impacted, as the Soviets would almost certainly have used their nuclear supremacy to their military advantage.

It should also be recognised that quantum computing has enormous potential for positive use cases, such as weather forecasting and health research.